As we have noted in the first section it is possible to transfer electrons between an electrode and a chemical species in solution. This process is called electrolysis and results in a reactant undergoing an oxidation or reduction reaction. Unlike equilibrium measurements recorded using a two electrode, two compartment cell, electrolysis results in the flow of current around an electrical circuit. This current can be controlled by a number of factors, the two most common are:
- The rate of electron transfer between the metal and species in solution
- The transport of material to and from the electrode interface
Kinetics of Electron Transfer
In this section we will develop a quantitative mThe current flowing in either the reductive or oxidative steps can be predicted using the following expressions odel for the influence of the electrode voltage on the rate of electron transfer. For simplicity we will consider a single electron transfer reaction between two species (O) and (R)
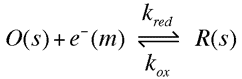
The current flowing in either the reductive or oxidative steps can be predicted using the following expressions
![]()
![]()
and so the corresponding reaction rates are given by
For the reduction reaction the current (ic) is related to the electrode area (A), the surface concentration of the reactant [O]o, the rate constant for the electron transfer (kRed or kOx) and Faraday's constant (F). A similar expression is valid for the oxidation, now the current is labelled (ia), with the surface concentration that of the species R. Similarly the rate constant for electron transfer corresponds to that of the oxidation process. Note that by definition the reductive current is negative and the oxidative positive, the difference in sign simply tells us that current flows in opposite directions across the interface depending upon whether we are studying an oxidation or reduction. To establish how the rate constants kOx and kRed are influenced by the applied voltage we will use transition state theory from chemical kinetics. You will recall that in this theory the reaction is considered to proceed via an energy barrier. The summit of this barrier is referred to as the transition state.
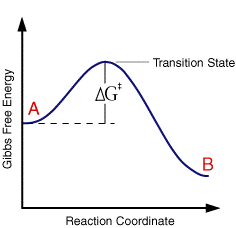
The rate of reaction for a chemical process (eg)
![]()
is predicted by an equation of the form
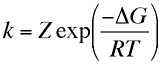
where the term in the exponential is the free energy change in taking the reactant from its initial value to the transition state divided by the temperature and gas constant. This free energy plot is also qualitatively valid for electrode reactions
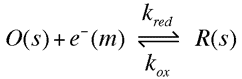
where the free energy plot below corresponds to the thermodynamic response at a single fixed voltage.
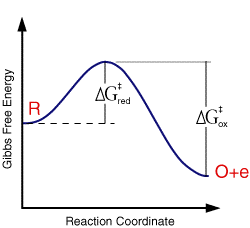
Using this picture the activation free energy for the reduction and oxidation reactions are
![]()
![]() and so the corresponding reaction rates are given by
and so the corresponding reaction rates are given by
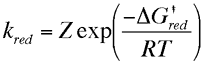
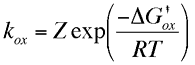
So for a single applied voltage the free energy profiles appear qualitatively to be the same as corresponding chemical processes. However if we now plot a series of these free energy profiles as a function of voltage it is apparent that the plots alter as a function of the voltage. It is important to note that the left handside of the figure corresponding to the free energy of R is invariant with voltage, whereas the right handside (O + e) shows a strong dependence.
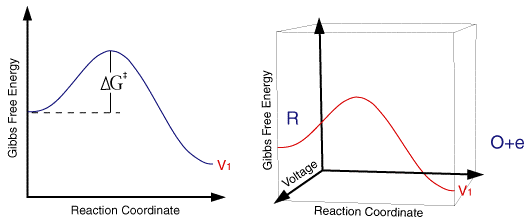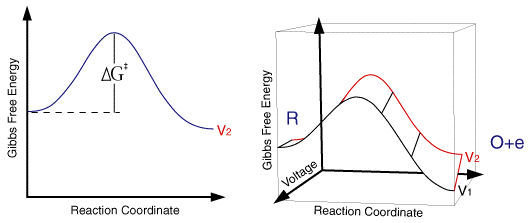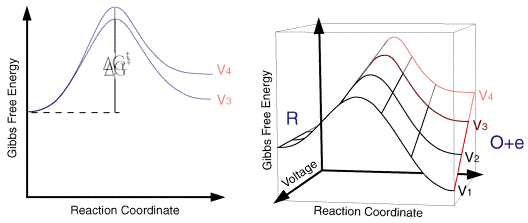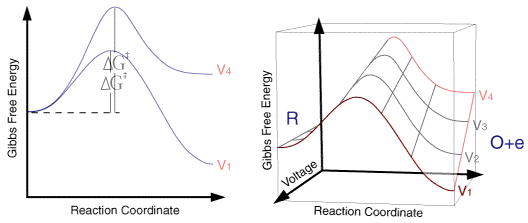
At voltage V1 the formation of the species O is thermodynamically favoured. However as we move through the voltages to V6 the formation of R becomes the thermodynamically favoured product. This can be explained in terms of the Fermi level diagrams noted earlier, as the voltage is altered the Fermi level is raised (or lowered) changing the energy state of the electrons. However it is not just the thermodynamic aspects of the reaction that can be influenced by this voltage change as the overall barrier height (ie activation energy) can also be seen to alter as a function of the applied voltage. We might therefore predict that the rate constants for the forward and reverse reactions will be altered by the applied voltage. In order to formulate a model we will assume that the effect of voltage on the free energy change will follow a linear relationship (this is undoubtedly an over simplification). Using this linear relationship the activation free energies for reduction and oxidation will vary as a function of the applied voltage (V) as follows
![]()
![]()
The parameter α is called the transfer coefficient and typically is found to have a value of 0.5. Physically it provides an insight into the way the transition state is influenced by the voltage. A value of one half means that the transition state behaves mid way between the reactants and products response to applied voltage. The free energy on the right hand side of both of the above equations can be considered as the chemical component of the activation free energy change, ie it is only dependent upon the chemical species and not the applied voltage. We can now substitute the activation free energy terms above into the expressions for the oxidation and reduction rate constants, which gives
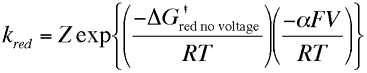
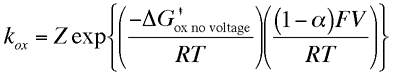
These results show us the that rate constants for the electron transfer steps are proportional to the exponential of the applied voltage. So the rate of electrolysis can be changed simply by varying the applied voltage. This result provides the fundamental basis of the experimental technique called voltammetry which we will look at more closely later.
In conclusion we have seen that the rate of electron transfer can be influenced by the applied voltage and it is found experimentally that this behaviour can be quantified well using the simple model presented above. However the kinetics of the electron transfer is not the only process which can control the electrolysis reaction. In many circumstances it is the rate of transport to the electrode which controls the overall reaction.

