Linear Sweep and Cyclic Voltametry: The Principles

In this section two closely related forms of voltammetry are introduced

• Linear Sweep Voltammetry
• Cyclic Voltammetry

We shall see how these measurements can be employed to study the electron transfer kinetics and transport properties of electrolysis reactions.

Linear Sweep Voltammetry

In linear sweep voltammetry (LSV) a fixed potential range is employed much like potential step measurements. However in LSV the voltage is scanned from a lower limit to an upper limit as shown below.

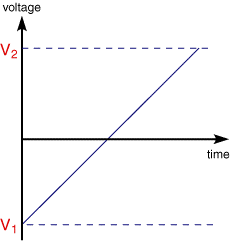
The voltage scan rate (v) is calculated from the slope of the line. Clearly by changing the time taken to sweep the range we alter the scan rate. The characteristics of the linear sweep voltammogram recorded depend on a number of factors including:

• The rate of the electron transfer reaction(s)
• The chemical reactivity of the electroactive species
• The voltage scan rate

In LSV measurements the current response is plotted as a function of voltage rather than time, unlike potential step measurements. For example if we return to the Fe3+/Fe2+ system

then the following voltammogram would be seen for a single voltage scan using an electrolyte solution containing only Fe3+ resulting from a voltage sweep

The scan begins from the left hand side of the current/voltage plot where no current flows. As the voltage is swept further to the right (to more reductive values) a current begins to flow and eventually reaches a peak before dropping. To rationalise this behaviour we need to consider the influence of voltage on the equilibrium established at the electrode surface. If we consider the electrochemical reduction of Fe3+ to Fe2+, the rate of electron transfer is fast in comparsion to the voltage sweep rate. Therefore at the electrode surface an equilibrum is established identical to that predicted by thermodynamics. You may recall from equilibrium electrochemistry that the Nernst equation:

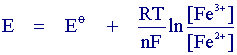
predicts the relationship between concentration and voltage (potential difference), where E is the applied potential difference and Eo is the standard electrode potential. So as the voltage is swept from V1 to V2 the equilibrium position shifts from no conversion at V1 to full conversion at V2 of the reactant at the electrode surface. The exact form of the voltammogram can be rationalised by considering the voltage and mass transport effects. As the voltage is initially swept from V1 the equilibrium at the surface begins to alter and the current begins to flow: 

The current rises as the voltage is swept further from its initial value as the equilibrium position is shifted further to the right hand side, thus converting more reactant. The peak occurs, since at some point the diffusion layer has grown sufficiently above the electrode so that the flux of reactant to the electrode is not fast enough to satisfy that required by the Nernst equation. In this situation the curent begins to drop just as it did in the potential step measurements. In fact the drop in current follows the same behaviour as that predicted by the Cottrell equation.

The above voltammogram was recorded at a single scan rate. If the scan rate is altered the current response also changes. The figure below shows a series of linear sweep voltammograms recorded at different scan rates for an electrolyte solution containing only Fe3+  

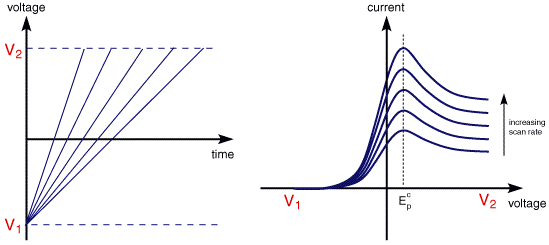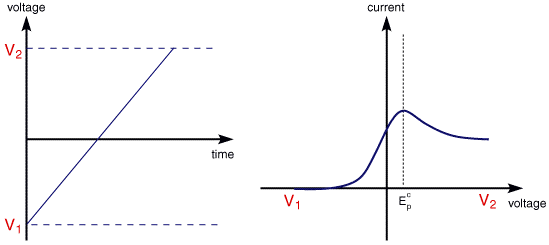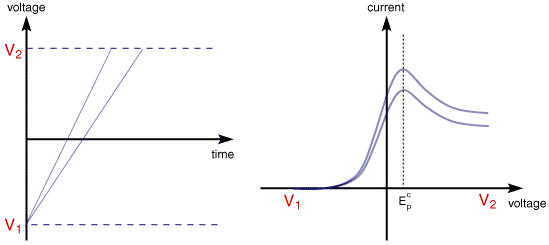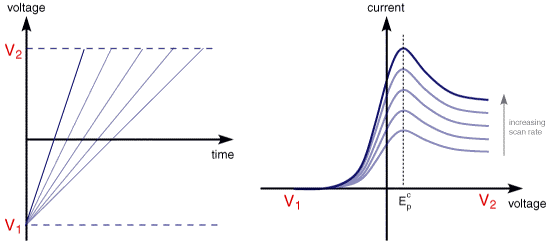
Each curve has the same form but it is apparent that the total current increases with increasing scan rate. This again can be rationalised by considering the size of the diffusion layer and the time taken to record the scan. Clearly the linear sweep voltammogram will take longer to record as the scan rate is decreased. Therefore the size of the diffusion layer above the electrode surface will be different depending upon the voltage scan rate used. In a slow voltage scan the diffusion layer will grow much further from the electrode in comparison to a fast scan. Consequently the flux to the electrode surface is considerably smaller at slow scan rates than it is at faster rates. As the current is proportional to the flux towards the electrode the magnitude of the current will be lower at slow scan rates and higher at high rates. This highlights an important point when examining LSV (and cyclic voltammograms), although there is no time axis on the graph the voltage scan rate (and therefore the time taken to record the voltammogram) do strongly effect the behaviour seen. A final point to note from the figure is the position of the current maximum, it is clear that the peak occurs at the same voltage and this is a characteristic of electrode reactions which have rapid electron transfer kinetics. These rapid processes are often referred to as reversible electron transfer reactions.

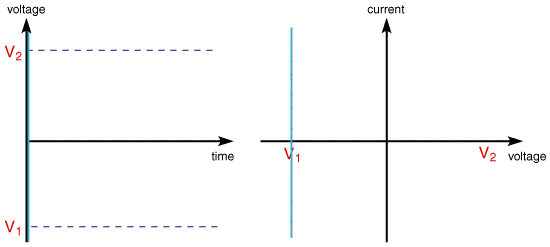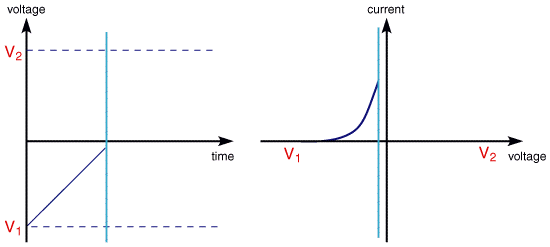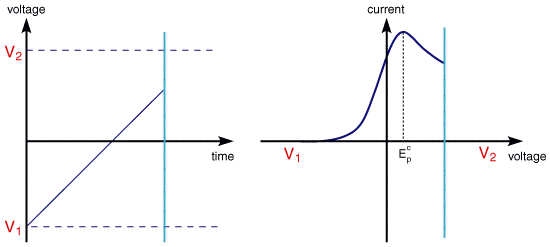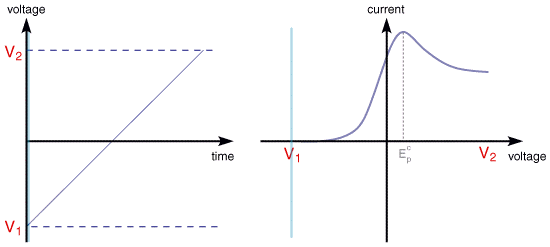
This leaves the question as to what would happen if the electron transfer processes were 'slow' (relative to the voltage scan rate). For these cases the reactions are referred to as quasi-reversible or irreversible electron transfer reactions. The figure below shows a series of voltammograms recorded at a single voltage sweep rate for different values of the reduction rate constant (kred)

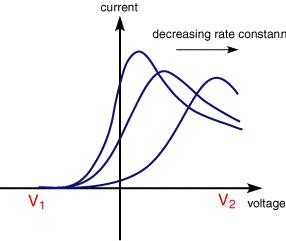
In this situation the voltage applied will not result in the generation of the concentrations at the electrode surface predicted by the Nernst equation. This happens because the kinetics of the reaction are 'slow' and thus the equilibria are not established rapidly (in comparison tothe voltage scan rate). In this situation the overall form of the voltammogram recorded is similar to that above, but unlike the reversible reaction now the position of the current maximum shifts depending upon the reduction rate constant (and also the voltage scan rate). This occurs because the current takes more time to respond to the the applied voltage than the reversible case.

Cyclic Voltammetry

Cyclic voltammetry (CV) is very similar to LSV. In this case the voltage is swept between two values (see below) at a fixed rate, however now when the voltage reaches V2 the scan is reversed and the voltage is swept back to V1

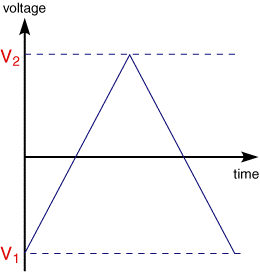
A typical cyclic voltammogram recorded for a reversible single electrode transfer reaction is shown in below. Again the solution contains only a single electrochemical reactant

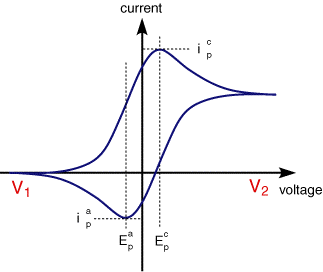
The forward sweep produces an identical repsonse to that seen for the LSV experiment. When the scan is reversed we simply move back through the equilibrium positions gradually converting electrolysis product (Fe2+ back to reactant (Fe3+). The current flow is now from the solution species back to the electrode and so occurs in the opposite sense to the forward seep but otherwise the behaviour can be explained in an identical manner. For a reversible electrochemical reaction the CV recorded has certain well defined characteristics.

I) The voltage separation between the current peaks is

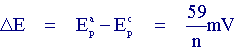
II) The positions of peak voltage do not alter as a function of voltage scan rate

III) The ratio of the peak currents is equal to one

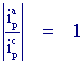
IV) The peak currents are proportional to the square root of the scan rate

As with LSV the influence of scan rate is explained for a reversible electron transfer reaction in terms of the diffusion layer thickness.

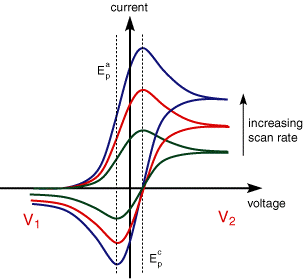
The CV for cases where the electron transfer is not reversible show considerably different behaviour from their reversible counterparts. The figure below shows the voltammogram for a quasi-reversible reaction for different values of the reduction and oxidation rate constants.

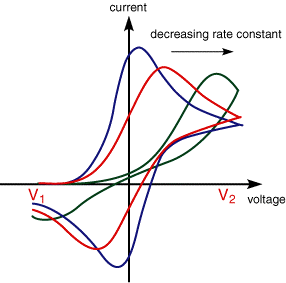
The first curve shows the case where both the oxidation and reduction rate constants are still fast, however, as the rate constants are lowered the curves shift to more reductive potentials. Again this may be rationalised interms of the equilibrium at the surface is no longer establishing so rapidly. In these cases the peak separation is no longer fixed but varies as a function of the scan rate. Similarly the peak current nolonger varies as a function of the square root of the scan rate.

By analysing the variation of peak position as a function of scan rate it is possible to gain an estimate for the electron transfer rate constants.