In the electrode kinetics section we have seen that the rate of reaction can be influenced by the cell potential difference. However, the rate of transport to the surface can also effect or even dominate the overall reaction rate and in this section we look at the different forms of mass transport that can influence electrolysis reactions.
We have already seen that a typical electrolysis reaction involves the transfer of charge between an electrode and a species in solution. This whole process due to the interfacial nature of the electron transfer reactions typically involves a series of steps.
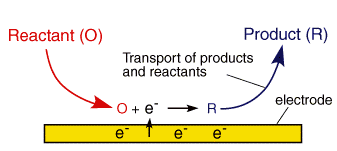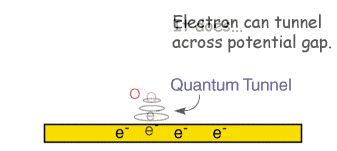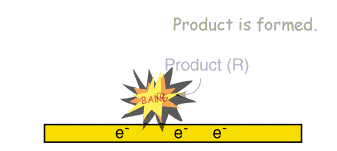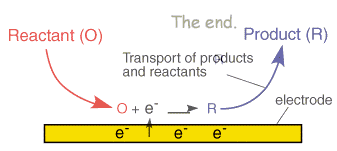
In the section on electrode kinetics we saw how the electrode voltage can effect the rate of the electron transfer. This is an exponential relationship, so we would predict from the electron transfer model that as the voltage is increased the reaction rate and therefore the current will increase exponentially. This would mean that it is possible to pass unlimited quantities of current. Of course in reality this does not arise and this can be rationalised by considering the expression for the current that we encountered in the electrode kinetics section
![]()
Clearly for a fixed electrode area (A) the reaction can be controlled by two factors. First the rate constant kred and second the surface concentration of the reactant ([O]o). If the rate constant is large, such that any reactant close to the interface is immediately converted into products then the current will be controlled by the amount of fresh reactant reaching the interface from the bulk solution above. Thus movement of reactant in and out of the interface is important in predicting the current flowing. In this section we look at the various ways in which material can move within solution - so called mass transport.
There are three forms of mass transport which can influence an electrolysis reaction:
- Diffusion
- Convection
- Migration
In order to predict the current flowing at any particular time in an electrolysis measurement we will need to have a quantitative model for each of these processes to complement the model for the electron transfer step(s).
Diffusion
Diffusion occurs in all solutions and arises from local uneven concentrations of reagents. Entropic forces act to smooth out these uneven distributions of concentration and are therefore the main driving force for this process. One example of this can be seen in the animation below. Two materials are held separately in a single container separated by a barrier. When the barrier is removed the two reagents can mix and this processes on the microscopic scale is essentially random. For a large enough sample statistics can be used to predict how far material will move in a certain time - and this is oftern referred to as a random walk model.
Diffusion is particularly significant in an electrolysis experiment since the conversion reaction only occurs at the electrode surface. Consequently there will be a lower reactant concentration at the electrode than in bulk solution. Similarly a higher concentration of product will exist near the electrode than further out into solution.
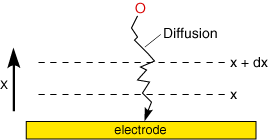
The rate of movement of material by diffusion can be predicted mathematically and Fick proposed two laws to quantify the processes. The first law:
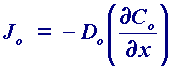
relates the diffusional flux Jo (ie the rate of movement of material by diffusion) to the concentration gradient and the diffusion coefficient Do. The negative sign simply signifies that material moves down a concentration gradient ie from regions of high to low concentration. However, in many measurements we need to know how the concentration of material varies as a function of time and this can be predicted from the first law. The result is Fick's second law
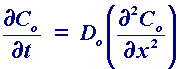
In this case we consider diffusion normal to an electrode surface (x direction). The rate of change of the concentration ([O]) as a function of time (t) can be seen to be related to the change in the concentration gradient. So the steeper the change in concentration the greater the rate of diffusion. In practice diffusion is often found to be the most significant transport process for many electrolysis reactions.
Fick's second law is an important relationship since it permits the prediction of the variation of concentration of different species as a function of time within the electrochemical cell. In order to solve these expressions analytical or computational models are usually employed.
Convection
Convection results from the action of a force on the solution. This can be a pump, a flow of gas or even gravity. There are two forms of convection the first is termed natural convection and is present in any solution. This natural convection is generated by small thermal or density differences and acts to mix the solution in a random and therefore unpredictable manner. In the case of electrochemical measurements these effects tend to case problems if the measurement time for the experiment exceeds 20 seconds.
It is possible to drown out the natural convection effects from an electrochemical experiment by deliberately introducing convection into the cell. This form of convection is termed forced convection. It is typically several orders of magnitude greater than any natural convection effects and therefore effectively removes the random aspect from the experimental measurements. This of course is only true if the convection is introduced in a well defined and quantitative manner. We will see in later sections examples of such systems, including the rotating disc and wall jet electrodes. In each of these devices the convection is introduced so that a laminar flow profile created.
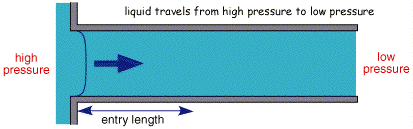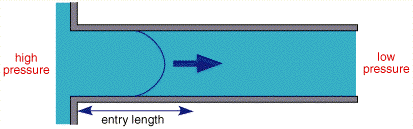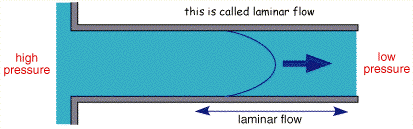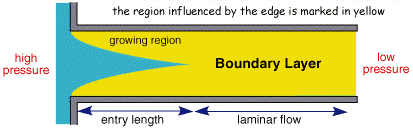
The figure above shows the cross section of liquid flowing through a pipe. Solution is introduced from the right handside and pumped through the pipe. If the flow is controlled, after a small lead in length, the profile will become stable with no mixing in the lateral direction, this is termed laminar flow.
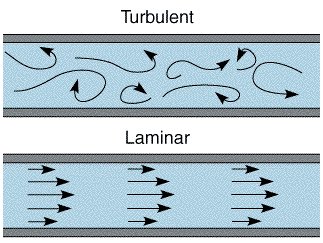
If however the solution is pumped through the cell at a high rate then the transport can become turbulent, where the solution movement is essentially a random and unpredictable. In order to predict this change over between turbulent and laminar behaviour, work was carried out by Hagan in the mid 1840's and later by Reynolds who was the first to put forward a predicitive model. In this particular example there is a maximum velocity in the centre and minimum velocity at the side walls. For laminar flow conditions the mass transport equation for (1 dimensional) convection is predicted by
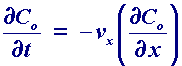
where vx is the velocity of the solution which can be calculated in many situations be solving the appropriate form of the Navier-Stokes equations. An analogous form exists for the three dimensional convective transport. When an electrochemical cell possesses forced convection we must be able to solve the electrode kinetic, diffusion and convection steps, to be able to predict the current flowing. This can be a difficult problem to solve even for modern computers and yet we still have one final form of mass transport to address!
Migration
The final form of mass transport we need to consider is migration. This is essentially an electrostatic effect which arises due the application of a voltage on the electrodes. This effectively creates a charged interface (the electrodes). Any charged species near that interface will either be attracted or repelled from it by electrostatic forces. The migratory flux induced can be described mathematically (in 1 dimension) using
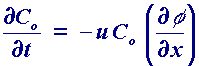
However due to ion solvation effects and diffuse layer interactions in solution, migration is notoriously difficult to calculate accurately for real solutions. Consequently most voltammetric measurements are performed in solutions which contain a background electrolyte - this material is a salt (eg KCl) that does not undergo electrolysis itself but helps to shield the reactants from migratory effects. By adding a large quantity of the electrolyte (relative to the reactants) it is possible to ensure that the electrolysis reaction is not significantly effected by migration. The purpose of introducing a background electrolyte into a solution is not however solely to remove migration effects as it also acts as a conductor to help the passage of current through the solution.
Mass Transport in Electrochemical Cells
To gain a quantitative model of the current flowing at the electrode we must account for the electrode kinetics, the 3 dimensional diffusion, convection and migration, of all the species involved. This is currently beyond the capacity of even the fastest computers - and will be for some time. However, as we will discover later electrochemical cells and experimental conditions can be employed to cheat the mass transport equations. We can effectively remove much (but not all) of the mass transport complexity by carefully designing and controlling the electrochemical experiment.

