In the discussion of electron transfer reactions so far there has been no mention of the nature of the electrode/electrolyte interface. It is clear that any interface will disrupt the electrolyte solution since the interactions between the solid and the electrolyte will be considerably different to those in solution. For electrodes which are under potentiostatic control there will also be the additional influence of the charge held at the electrode. These different factors result in strong interactions occurring between the ions/molecules in solution and the electrode surface. This gives rise to a region called the electrical double layer. Many models have been put forward to explain the behaviour observed when electrochemical measurements are performed in electrolyte solutions. Below we introduce two of the models which have been used to explain the effects occurring in this region.
The Electrical Double Layer
The model which gave rise to the term 'electrical double layer' was first put forward in the 1850's by Helmholtz. In this model he assumed that no electron transfer reactions occur at the electrode and the solution is composed only of electrolyte. The interactions between the ions in solution and the electrode surface were asssumed to be electrostatic in nature and resulted from the fact that the electrode holds a charge density (qm)which arises from either an excess or deficiency of electrons at the electrode surface. In order for the interface to remain neutral the charge held on the electrode is balanced by the redistribution of ions close to the electrode surface. Helmholtz's view of this region is shown in the figure below
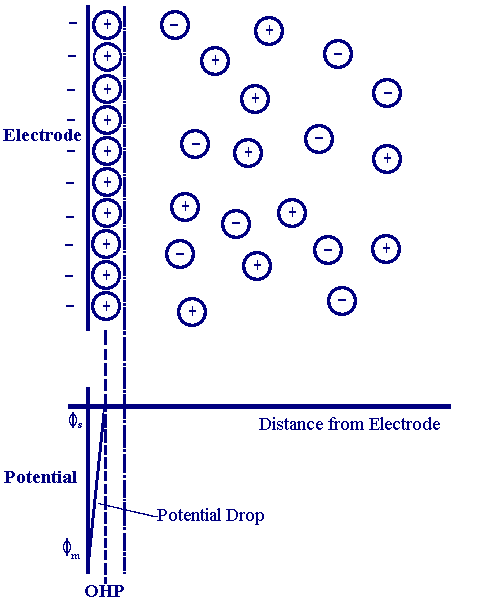
The attracted ions are assumed to approach the electrode surface and form a layer balancing the electrode charge, the distance of approach is assumed to be limited to the radius of the ion and a single sphere of solvation round each ion. The overall result is two layers of charge (the double layer) and a potential drop which is confined to only this region (termed the outer Helmholtz Plane, OHP) in solution. The result is absolutely analogous to an electrical capacitor which has two plates of charge separated by some distance (d)
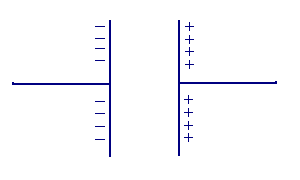
with the potential drop occurring in a linear manner between the two plates. It is perhaps no surprise that when impedance analysis is performed on electrochemical systems the response due to the electrolyte redistribution is modelled in terms of capacitative elements.
The model of Helmholtz while providing a basis for rationalising the behaviour of this region does not account for many factors such as, diffusion/mixing in solution, the possibility of absorption on to the surface and the interaction between solvent dipole moments and the electrode. A later model put forward by Stern begins to address some of these limitations
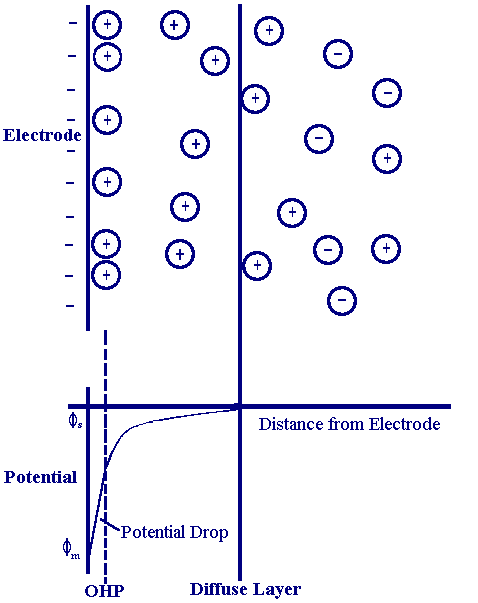
now the ions are assumed to be able to move in solution and so the electrostatic interactions are in competition with Brownian motion. The result is still a region close to the electrode surface (100x10-10 m) containing an excess of one type of ion but now the potential drop occurs over the region called the diffuse layer.
Many modifications and improvements have been made to these early models with the latest approaches using numerical modelling to follow the redistribution effects as the electrode potential is varied.

