Heat transfer has been investigated in a two pass reactor configuration, using a light mineral oil pumped through the tube side and water in the shell as the cooling fluid at a high enough flowrate to ensure that the limit to heat transfer was on the tube side. We have investigated the heat transfer coefficient (Nusselt number) as a function of the oscillatory flow component superimposed on a bulk flow in a low Re region, i.e. Ren < 1000, which would correspond laminar flow in a smooth tube.
The figure below shows the results, where the Nusselt Number (Nu) is plotted against the bulk flow Reynolds number. The oscillatory conditions 0, 6, 8, and 10Hz frequencies at a fixed amplitude of 5mm are shown, corresponding to an oscillatory Reynods number = 0 (steady flow), 950, 1250, and 1590 respectively. Also shown are standard heat transfer correlations for laminar and turbulent flow assuming smooth tube with steady flow. This gives an overview of the heat transfer regimes corresponding to different types of flow behaviour.
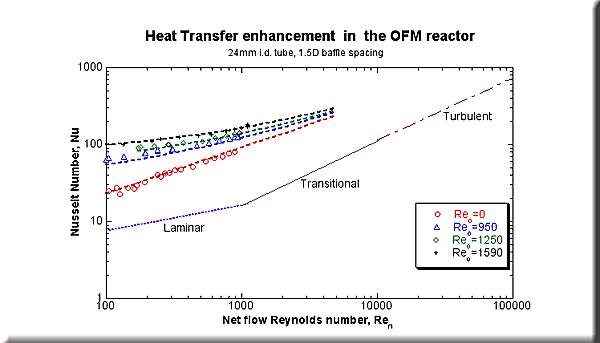 |
It can be seen that for a given throughput (i.e. net flow Reynolds number), the heat transfer increases with increasing oscillatory Reynolds numbers. At high throughput, the oscillatory curves approach the steady flow curve, as the net flow component becomes larger relative to the oscillatory flow component. However, at low values of net flow, high rates of heat transfer are still obtainable provided the oscillatory flow component is present. For example, for an oscillatory Reynolds number=1590, it can be seen that the Nusselt number is of order 120 where the net flow Reynolds number=200. This corresponds to heat transfer which may be obtained from turbulent flow in a smooth tube where Ren =10 000.
In order to provide a design correlation for oscillatory flow heat transfer, we have modelled the heat transfer data phenomenologicaly, as follows:
The correlation is plotted as dotted lines on the graph for all the data, and it can be seen that the behaviour is predicted with reasonable accuracy experimental range. The first term of the correlation corresponds to the steady flow contribution to heat transfer, and is similar to the well-known Dittus Boelter turbulent flow equation, but the exponent of Ren is different to account for the effect of the baffles. The second term includes the oscillatory behaviour, by assuming that the effect of oscillation can be accounted for by adding the oscillatory term to the steady term. In the case for steady flow, the correlation reduces to the baffles only curve plotted on the graph. When the net flow Reynolds number is much greater than the oscillatory flow Reynolds number, the oscillatory term is small in relation to the steady term, and the curve collapses onto the steady flow behaviour again. In contrast, when the thoughput is zero, batch heat transfer will be predicted by the non-zero second term. This correlation can be used to calculate Nu in the reactor tube a priori, given the net flow and oscillatory conditions.
Conclusions
It is clear from these results that Oscillatory Flow Mixing has a significant enhancement effect on tube-side heat transfer, particularly in the low Reynolds number throughput regime, which would correspond to long residence times in the reactor. Furthermore, the heat transfer enhancement can be controlled by the oscillatory mixing independently of any net flow, and in this respect, oscillatory flow reactor offers a strategic advantage over static mixer reactors which would not offer the same degree of thermal control.

